 リッチー
リッチーどうも!リッチーです!



やあやあ!サトシだよ!
2021年12月24日に公開された映画が、エヴァンゲリオンを超える興行収入ペースであることが報じられた「呪術廻戦」。
幅広い世代に人気を誇る呪術廻戦で、特に人気のキャラクターが「五条悟」です。
圧倒的な強さと、そのカッコよさから絶大な人気を誇っています。
そんな五条悟が最強たるゆえんとして、「無限」がキーワードとなってきます。
ところが、この無限というものは非常に奥が深く理解するのは簡単ではありません。
今回は、そんな「無限」という概念について、わかりやすく解説します。
「無限」とは?
「無限」とはなにか。
長年数学者を悩ませ続けてきた問題のひとつに、「無限」というものがあります。
実は、僕の卒業研究テーマである「ブラックホール」にも多少絡んできます。
ブラックホールについては、下記の記事も読んでみてください!
今回は、「無限」についてある程度ざっくりした説明をしたいと思います。
「無限」に興味がある方は、こちらの雑誌を読んでみると面白いかもしれません。
▶︎▶︎▶︎Newton別冊『無とは何か』 (ニュートン別冊)



厳密に無限を説明しようとすると、超難解!



簡単に説明してくれ〜!



オッケー!
無限をひとことで表すとするなら、「数や量に限りがないこと」となります。
文字だと非常に簡単のように感じますが、実際にイメージしようとするとそう簡単ではありません。



要は、限りなく大きい数のことでしょ?



実は、そんな単純な話じゃないんだ!
無限と聞いて想像するであろう「限りなく大きな数」とは、全く違います。
「限りなく大きな数」はあくまで大きな数であり有限の値です。
有限とは、数に限りがあることですから先ほどの無限の説明に反していることになります。
無限が「限りがないことである」ということは、言葉で聞くと非常に簡単です。
実際にイメージしようとすると、無限ほどイメージしにくいものはあまりないのではないでしょうか。



やばい・・・
すでに分からなくなってきた
「すでに分からん!もう読みたくない!」
そう思うのも無理もありません。
2,000年以上前から議論されてきた「無限」をそう簡単に理解できるはずもないのです。



僕でも難しいよ!!
今回は、無限とは「有限の反対で限りがないこと」という認識で十分です。
それさえわかっていれば理解できるように、できるだけわかりやすく解説していくのでぜひ最後まで読んでみてくださいね。



頑張るぞー!
アキレスと亀のパラドックス
まずは「アキレスと亀」について。
この問題は、数学のパラドックスを考える上で非常に重要な問題です。



え、実際には追いつけるじゃん!



これが「アキレスと亀」の難しいところ!
実はこれ、「アキレスと亀のパラドックス」と呼ばれる数学的には有名な問題。
「どこに無限が出てくるの?」と思った方もいたかもしれません。
このパラドックスを説明するのが、次の章で説明する「無限級数」なのです。
無限級数
無限級数は、高校数学で学ぶことのひとつです。
しかし、そのイメージのしにくさなどから、苦手とする人が非常に多いのがこの分野なのです。



塾講師である僕も、教えるのに苦労してるよ!
無限級数を理解するためには、まずは「数列」を理解しなければなりません。
なるべくわかりやすくするために、イチから解説していきます。
数列とは
数列とは、簡単に言えば「数が並んだ列のこと」です。
「1、2、3、・・・」というように数が並んでいるものが数列になります。
さらに厳密に言えば、「一定の規則に従って並んだ数の列」が数列の定義となります。
数列のひとつひとつの数を「項」とよび、1番最初の項を初項といいます。
初項から順に、第二項、第三項、・・・と呼ぶのが一般的です。



すでに難しい・・・



いったんまとめよう!
数列といっても様々な種類があります。
今回考える数列は、「等比数列」と呼ばれるもの。
等比数列は、隣どうしの項の比が一定となるような数列のことです。



比?イメージできないな・・・



わかりやすく図で見ていこう!
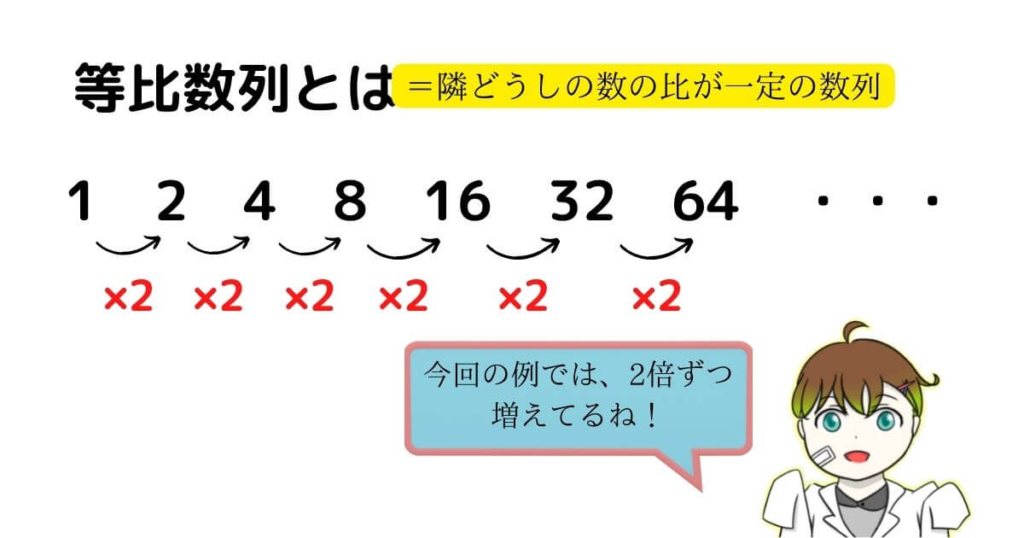

比とは、どれくらいの割合で増えているか(減っているか)を表す数のこと。
今回の場合は、2倍ずつ増えているので比は2となります。



この比がずっと一緒なのが等比数列だよ!



ずっと?



ず〜〜〜〜〜っと!
無限級数
これまで、等比数列に関して考えてきました。
今回考えるのは、その等比数列の「和」です。
例えば、先ほどのアキレスと亀の例を考えましょう。
亀が進む距離が9m、0.9m、0.09m、0.009m、・・・という等比数列があったとしましょう。
亀が進んだ距離の合計は、この等比数列の和であり、「等比級数」という呼び方があります。
実際に、この等比級数は


と計算することができます。
今回の等比級数のように、終わりがないものを「無限(等比)級数」と呼びます。
実際に計算を進めていくと、9.999…と小数点以下に無限に9が続くこととなります。
極限の考え方を使うと、9.999…=10となるのですが・・・
この説明に関しては、こちら(ページ内リンク)をご覧ください。



ここでは9.999…=10ということにしてね!
また、アキレスと亀の距離を90mと仮定しましょう。
アキレスは、90m、9m、0.9m、0.09m、・・・と進むとします。
先ほどの亀と同様に考えると、アキレスが進んだ距離の合計は90+9+0.9+0.09+…=99.999…となります。
つまり、99.999…=100m進んだことになります。



納得できん・・・



ここは我慢して〜!
最終的に亀は10m、アキレスは100m進んだこととなるわけです。
アキレスと亀が、最初90m離れていたことをふまえると、アキレスは亀に100mの地点で追いつくこととなります。
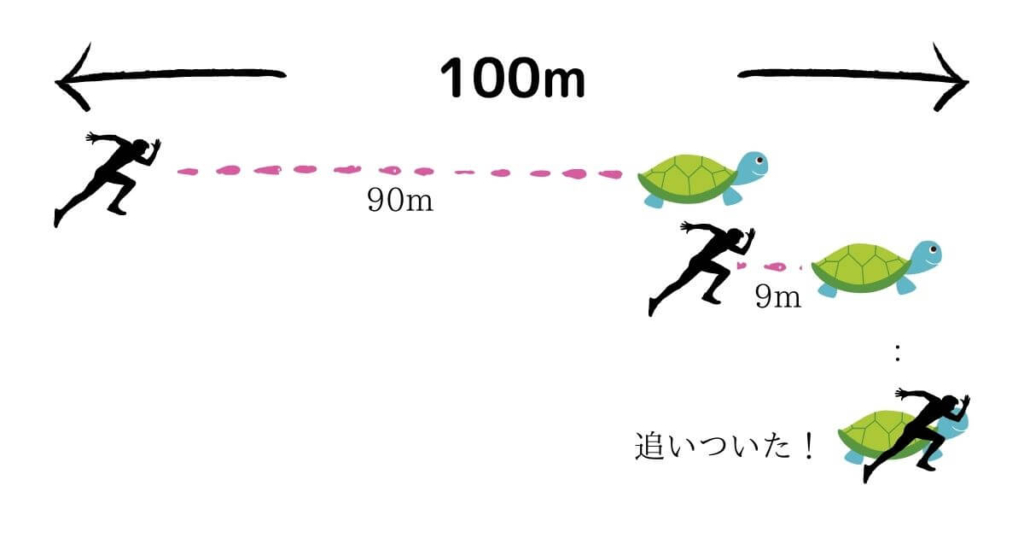

とはいえ、今回の説明ではいろいろ省略してしまっています。
9.999…=10など、納得いかない考え方があると思いますが、ここではいったん置いておきます。
今回省略したことに関しては、次の章以降で説明することしましょう。
収束と発散
無限級数を考えるにあたって重要となってくるのが、「収束」と「発散」です。



「収束」と「発散」について簡単にまとめるとこんな感じ!
「収束」は、ある一定の値に近づいていくこと。
「発散」は、値が無限大(正の無限大:+∞、負の無限大:-∞)になること。
発散とは
まずは、比較的簡単な「発散」から考えていきます。
発散とは、簡単に言えば値がどんどん大きくなっていく(または小さくなっていく)ことを表します。
例えば、初項が1、公比が2無限等比数列があったとします。
項の数は「無限」個ですから、数列の項の値は非常に大きなものとなります▼


これが発散です。
ちなみに、初項が負の数(マイナスの数:例えば -3 とか)の場合には、負の無限大 -∞ になります。



初項とか公比とかごちゃごちゃになってきた…



もう一回復習しよう!
収束とは
発散ほど簡単な話ではないのが、「収束」です。
言葉で説明すると、「一定の値に近づくこと」が収束です。
しかし、なかなかイメージが難しいのが収束です。
簡単にイメージするために、1枚の写真をお見せします。


面積が1である正方形を考えます。
面積を1/2、1/4、1/8、…と面積を半分にしていくと、いずれは面積が0に近づきます。
これが、「収束する」ということです。
また、図に注目すると、面白いことがわかります。
1/2+1/4+1/8+…と無限に足していくと、いずれは1に近づいていくのです。
今回の例は、初項1/2、公比1/2の等比数列です。
先ほどの収束の話をより数学的に言うとこんな感じとなります。
初項1/2、公比1/2の等比数列は、0に収束する。
また、この無限等比級数は1に収束する。



なんとなくわかったかも!
さらに詳しく…
今回紹介した「無限級数」と「収束と発散」の説明はあくまで噛み砕いたもの。
そのため、数学的に厳密ではない部分や少しわかりにくく感じる部分もあったと思います。



実力不足で申し訳ない!
数学的に説明すると、少し難しい説明となってしまいます。
一応、その説明を載せておきますが、難しいと思ったら読み飛ばしていただいて結構です。



ここまで理解できたら大丈夫!
「無限」は言葉以上に難しい
今回紹介してきた通り、「無限」という概念は非常に難しいのです。
無限とは、言葉以上にイメージするのが難しい概念です。
長年、無限の扱い方は数学者を悩ませてきました。



ほんっと頭が混乱するよ!
ここで、さらに不思議に思えることをひとつ紹介します。
非常にシンプルですが、「無限」について考えるには実に面白い問題です。
その問題がこちら▼
0.9999999…と1は等しいか?



1÷3は?



馬鹿にしてる!?
1÷3の答えは、2通りが考えられるのではないでしょうか。
その答えがこちら▼


2通りの表し方があり、混乱するかもしれませんが、どちらも正解です。
問題は1÷3の答えではありません。



え!?違うの!?
「1÷3」は、1を3等分するということを意味します。
では、「1÷3×3」はどうなると思いますか?
1÷3が、1を3等分したものと考えるならば、1÷3×3=1となることに疑問はないはず。
ですが、1÷3の先ほどの2通りの表し方を考えると、このようになるのではないでしょうか▼


2通りの結果をふまえると、1=0.99999…ということになります。
実はこれ、「正しい」のです。



え、違うじゃん!
と思うかもしれませんが、数学的には正しいのです。
0.999…とは、小数点以下に無限に9が続くことを意味します。
無限に9が続く場合には、0.9999…=1ということができるのです。



不思議だよね
今回は、「1÷3」と言う割り切れない割り算の例を紹介しました。
「割り切れない」とは、小数点以下に「無限」に数字が並ぶこと。
この「割り切れない」というのも、無限を考える上で重要な概念なのです。
五条悟「無下限呪術」とは
やっと本題です。
「呪術廻戦」に出てくる五条悟が使う「無下限呪術」について。



やっとここまで辿り着けた・・・



前置きが長すぎたね(笑)
ここまで、「無限」についてなるべく噛み砕いて説明してきました。
途中、わかりやすさのために詳しい説明などを省いた部分もありましたが、それでもこの長さ。
やはり侮れませんね・・・。
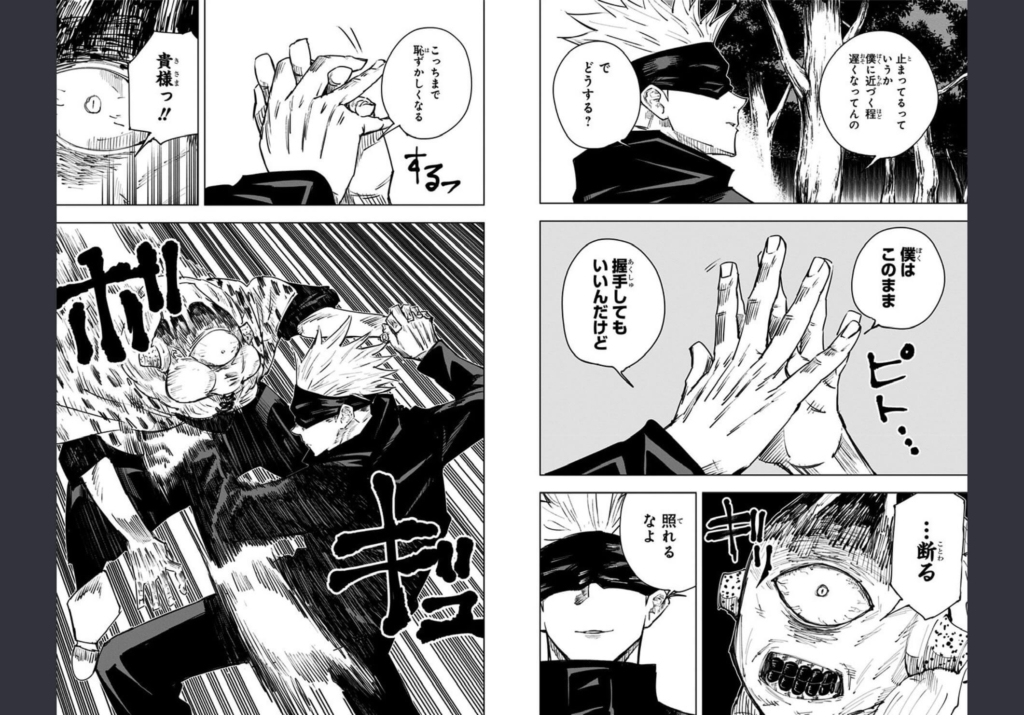

「呪術廻戦」の作中で、初めて五条悟が戦闘するシーン(「第14話 急襲」)において明かされたこと。
それが、「五条悟に近づくほど遅くなる」と。
これが意味するところは、先ほどの無限級数で説明することができます。



ここで無限級数が出てくるのか!
五条悟に近づくと、近づくスピードが徐々に遅くなる・・・。
これ、先ほどの「アキレスと亀」に非常によく似た話だと思いませんか?
五条悟を亀、五条悟に近づくものをアキレスと置き換えてみてください。
五条悟の術式は、アキレスが亀(五条悟)に近づくほど進む速さが小さくなるという「アキレスと亀」そのものです。
そして、このアキレスと亀の関係は、収束する無限級数によって説明することができます。
五条悟に近づくほどスピードが遅くなり、その速さはどんどん0に近づき(収束し)ます。
作中でも触れられている通り、「実際には止まっているわけではない」というのがポイント。
限りなく0に近いほどゆっくりと五条悟に近づいていることになります。



そう考えると、めっちゃ複雑だ…
作中では、かなり簡単に説明されています。
実際に説明しようとすると、かなり骨の折れる分野であることをおわかりいただけたでしょうか。
今回の説明がいまいち分からなくても大丈夫。
例え全く理解できなかったとしても、問題なく本編を楽しむことができます(笑)
これを機に、ぜひ読んでみてくださいね!
漫画はこちらから▼
また、Amazon Prime会員になれば、追加料金なしでprime videoを視聴可能。
呪術廻戦の大迫力のアニメを無料で見ることができます。
ぜひこちらも試してみてくださいね。
\Amazon Primeの無料体験はこちら!/



最後まで読んでくれてありがとう!
SNSの登録もよろしく!









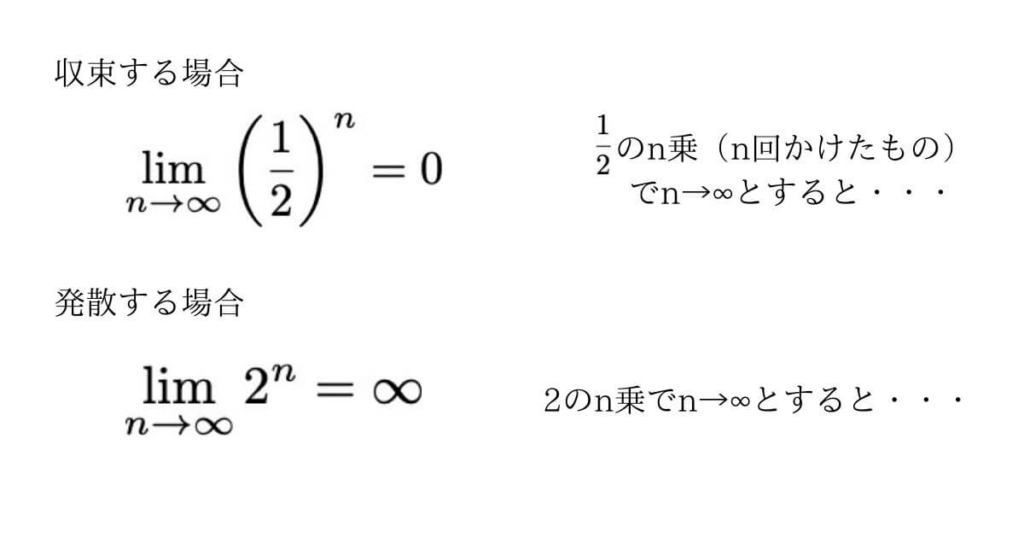



コメント